The other voting systems I’ve discussed in this series so far have been well-known in voting theory circles for at least half a century. The STAR voting system is a newcomer. To the best of my knowledge, the system was invented in 2014 by election reform activists, under the name score runoff voting. It combines a score vote (also known as a range vote) with an instant majority runoff using the same ballots.
Both the novelty of the method and the fact that it emerged from activist rather than scholarly circles mean that the formal voting theory literature on STAR voting is not very extensive. Out in the real world, the most prominent usage thus far has been in selecting Oregon’s delegates to the 2020 Democratic National Convention.
STAR voting is less complicated than ranked choice voting, but more complicated than an approval voting. The majority runoff stage helps ensures that a Condorcet loser will not win, but also means that the system is not always monotone. As with the Borda count, adoption of STAR voting requires a significant conceptual shift in how we think about votes. The system described in this article is designed for a single-winner election, although there is a variation designed for a proportional vote.
How STAR voting works
STAR voting takes place in two stages. The first stage is a score vote, also known as a range vote. The second stage is a majority runoff vote that uses the same ballots a second time. In terms of counting complexity, this is slightly more complex than a regular majority vote, but less complex than tabulating a ranked choice voting election with four or more candidates.
The score voting stage
Score voting is closely related to approval voting, but allows voters to express more granular preferences. Voters are asked to score (rate) candidates on a scale. The STAR voting website calls for the use of 0–5 points.
One of the major obstacles to the adoption of score voting on a 0-5 scale is that like using the traditional point values for a Borda count, this requires a conceptual shift from counting votes to adding up points or averaging ratings.
Since voters can freely give candidates the same rating, it is easier to rate candidates than to rank them: If a voter has trouble distinguishing between two candidates, they can give both of them the same score. As with other positional and multiple positional voting rules, a score vote is resolved by adding up all scores from all ballots. The candidate with the most points wins first place, the candidate with the second-most wins second place, et cetera.
From a purely theoretical perspective, score voting is generally similar to approval voting, except that it allows voters to express their preferences more finely. Unfortunately, if a score vote only elects a single winner, voters have a strong strategic incentive to only use the top and bottom scores, effectively casting an approval ballot. Things are different in a STAR vote, because the candidates with the top two scores advance to a runoff. I’ll discuss that in more detail later.
The majority runoff stage
In a STAR vote, the top two candidates from the score voting stage are selected for a runoff. Ballots must be re-examined at this point. Every ballot showing a different score for the two candidates is counted as a vote for one of those two candidates; ballots that do not show a score difference are ignored. The candidate with more votes wins.
This is not quite the same as holding a separate majority vote for two reasons. Separate runoffs often have reduced turnout and require additional effort from voters. Using the same ballots also makes it more difficult for voters to vote strategically. Using the same ballots makes the counting process slightly more complicated, and there are three different ways to handle this.
First, as with ranked choice voting, all ballot information can be combined and transmitted to a central tabulating location. Second, ballots can be stored and then recounted locally after central tabulation of the first round is complete. Third, local counting at the precinct level can pre-emptively include the preliminary tallies for each possible pair of candidates. This is only practical with a computerized counting system.
Strategic voting
Strategic voting in a STAR election is complicated by the fact that a voter or group of voters acting strategically needs to consider the possible impact of their ballot(s) in both rounds. Voters concerned their vote might not count in the second round need to be careful about how they act.
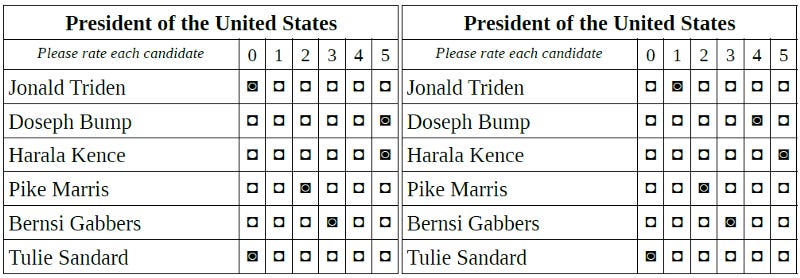
A voter with good information about which candidates are likeliest to win in the first round should use at a set of three different ratings for the three candidates they think are most likely to advance to the runoff, including the minimum (0) and maximum (5) scores. If their most preferred candidate is almost certain to make the runoff, they might use the highest intermediate rating (4) in order to prevent their least-favored candidate from winning; otherwise, they should use the lowest intermediate rating (1).
Based on my research in the area of multi-stage systems, I would say that the ballots that only use {0,1,5} give a generally greater risk of distorting the score voting round in an undesirable way, giving suboptimal results. My full reasoning is more complex than I want this article to be, but I will discuss one example of how widespread use of a strategic {0,1,5} ballot can backfire.
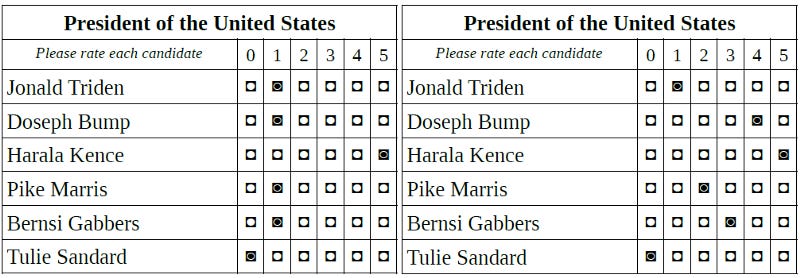
For example, suppose the candidates thought likeliest to win and also expected to place first and second are closely aligned with each other, as are the candidates expected to place third and fourth. Voters aligned with the top two candidates have an incentive to use strategic ballots of the {0,1,5} type to knock the other candidate out of the running and give them an easier match-up.
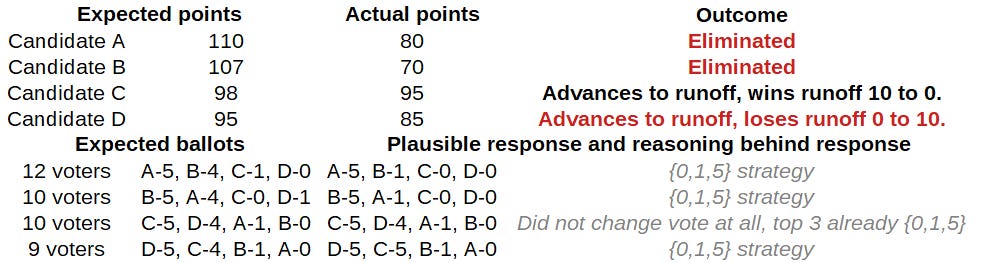
If there are enough of those ballots, and the other two candidates are not too far behind, this could bring both of them down far enough to knock them out of the runoff. Adding insult to injury, the elimination of both of these candidates in the first round would leave most of their strategic supporters with nothing but zero ratings left on their ballots during the runoff.
Much like the possible backfires from “burying” in a Borda count or “bullet voting” in an approval vote, this type of backfire relies a lot on many voters of certain types using first-level strategies but not higher-level strategies. (This exact example can be used with approval voting.)
Voters who aren’t sure what the results will look like have an incentive to spread their ratings out widely and make full use of the possible range of scores. For example, if a voter can distinguish between six different candidates and is unsure of the outcome of the first round, the correct move for them is to cast what is essentially a Borda ballot with <5,4,3,2,1,0> points — ensuring that their ballot is still counted in the majority runoff round no matter who advances.
Variations on a theme
In any “score then automatic runoff” process, the scale used in the score voting round matters. A very finely divided scale allows sincere voters to express more nuance in their ratings of candidates, but gives strategic voters more power and makes the ballot slightly more complex. The older proposal for STAR voting (as “Score Runoff Voting”) used 0-9 points. On the other end of the scale, the STAR system can operate in a meaningful way with as few as three possible scores.
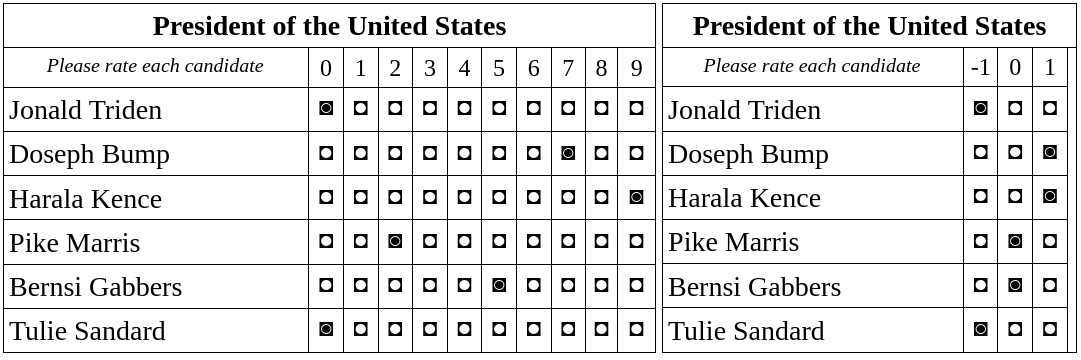
On a 0-5 scale, strategic voters would probably cast ballots using a subset of three possible scores, either {0,1,5} or {0,4,5}. On a 0-9 scale, strategic voters are likely to use scores drawn from either {0,1,9} or {0,8,9}. If the first round uses only three possible scores (e.g., {-1,0,1} in a combined approval vote), then strategic ballots will use the full range of possible scores.
Comparison with other voting systems
In some ways, analyzing score voting is very difficult, because voters have many more ways to try to achieve their desired outcome and strategic votes can look extremely different from sincere votes. More than any other type of voting system, the specific properties of score voting depend on how voters choose to behave.
As a result of this flexibility, as well as its hybrid nature as a scoring and ranking system, STAR voting nominally violates a number of axiomatic properties considered desirable for voting rules. Every multi-stage system violates monotonicity, for example; but this isn’t any more likely to happen in a STAR vote as opposed to a plurality vote with a majority runoff or a ranked choice vote. Similarly, it is theoretically possible for a Condorcet loser to win a STAR vote, but this requires a very unusual set of circumstances.
First, remember that one of the major concerns we identified above was strategic behavior that could lead most voters to use {0,1,5} ballots. If voters can easily identify the top three candidates and most voters cast strategic ballots of the {0,1,5} type, the system operates in a manner similar to a approval vote with a second separate majority runoff stage.
At the other end of the spectrum of strategic behavior, if voters use the whole set of ratings in a roughly symmetric fashion because they are unsure of the outcome in the score voting stage, then the results are very similar to using a Borda count with a linked majority runoff using the same ballots. Both approval voting and the Borda count are serious contenders in voting theory circles, and majority runoffs are useful safeguards for any system.
The main potential paths for poor outcomes with STAR voting come from cases where different groups of voters act very differently from each other or vote in ways that are very human but do not make strict strategic sense. The counting process for STAR voting requires two stages, and the first stage is more complex than most other counting processes other than that for a Borda count. However, for four or more candidates, this is still less complex than the counting process for ranked choice voting.
Summary
STAR voting is a newcomer to the world of proposed election system reforms. It’s a complicated design - a hybrid system that marries a score vote to a majority runoff. This helps address some of the potential problems present in score voting by encouraging voters to express preferences in greater depth. Like many alternatives to plurality, it is mostly untested, and we aren’t yet sure how voters will end up using the system in the long run.
It is complex to resolve because it requires counting ballots twice, but not much more complex than a plurality vote with a majority runoff. In elections with four or more candidates, the counting process is simpler than ranked choice voting.
From a naive theoretical perspective, STAR voting might seem terrible because it violates many deterministic criteria. However, from a more nuanced theoretical perspective, STAR voting seems likely to provide results similar to other theoretically promising systems if voters act in the sorts of ways that game theoretic analysis is likely to predict.
Finally, I will note that versions using a more finely gradiated scores allow slightly more nuance, while versions with fewer allowed scores - all the way down to a lower limit of three possible scores - would be both simpler to use and provide greater resistance to the effects of strategic voting. The best scale to use in the score voting stage may not be the same in all circumstances.